每天一道算法题🔥

2024-9-24 算法

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5 输出: 2 示例 2:

输入: nums = [1,3,5,6], target = 2 输出: 1 示例 3:

输入: nums = [1,3,5,6], target = 7 输出: 4 提示:

1 <= nums.length <= 104 -104 <= nums[i] <= 104 nums 为 无重复元素 的 升序 排列数组 -104 <= target <= 104 Related Topics 数组 二分查找

👍 2375 👎 0

第一次我写的算法

package leetcode.editor.cn;

import java.util.HashMap;
import java.util.Map;

//java:搜索插入位置
class P35SearchInsertPosition{
    public static void main(String[] args){
        Solution solution = new P35SearchInsertPosition().new Solution();
        System.out.println(solution.searchInsert(new int[]{1,3,5,6}, 2));
    }
    //leetcode submit region begin(Prohibit modification and deletion)
class Solution {
    public int searchInsert(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            map.put(i,nums[i]);
        }
        for (Integer i : map.keySet()) {
            if (i == 0 && map.get(i) > target){
                return 0;
            }
            if (map.get(i) == target){
                return i;
            }
            if (map.get(i) > target){
                return i;
            }
        }
        return nums.length;

    }
}
//leetcode submit region end(Prohibit modification and deletion)

}

呈现的效果

AI的分析与优化

你的代码目前在实现插入位置搜索时存在几个问题，特别是在使用时间复杂度为 O(log n) 的要求上。以下是详细分析和解决方案：

存在的问题：

1. 使用 HashMap： 你使用 HashMap 来存储数组索引和对应值，这样做不仅增加了不必要的空间复杂度，还使得查找的时间复杂度变为 O(n)。

2. 线性搜索： 你的循环遍历整个数组进行线性查找，虽然这对于较小数组是可行的，但在题目中要求使用 O(log n) 的时间复杂度。

3. 边界条件处理不当： 对于边界条件（如目标值小于数组的第一个元素或大于最后一个元素），你的实现没有高效处理。

解决方案：

要满足 O(log n) 的时间复杂度，可以使用二分查找。以下是更新后的代码：

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2; // 防止溢出
            if (nums[mid] == target) {
                return mid; // 找到目标值，返回索引
            } else if (nums[mid] < target) {
                left = mid + 1; // 目标值在右侧
            } else {
                right = mid - 1; // 目标值在左侧
            }
        }
        // 若未找到，返回插入位置
        return left; // 此时 left 即为目标值应该插入的位置
    }
}

代码解析：

1. 初始化边界： 定义两个指针 left 和 right，分别指向数组的开始和结束。

2. 二分查找： 在循环中计算中间索引 mid，并与目标值进行比较：

   • 如果 nums[mid] 等于目标值，直接返回 mid。
   • 如果 nums[mid] 小于目标值，则目标值在右侧，更新 left。
   • 如果 nums[mid] 大于目标值，则目标值在左侧，更新 right。

3. 插入位置返回： 如果循环结束后未找到目标值，left 就是目标值应该插入的位置。

总结：

通过使用二分查找的方法，你可以在 O(log n) 的时间复杂度内找到目标值或其插入位置，同时避免不必要的空间复杂度，提升代码的性能。

2024-9-25 算法

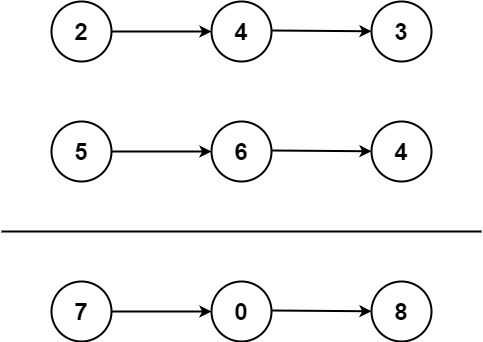
给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

• 每个链表中的节点数在范围 [1, 100] 内
• 0 <= Node.val <= 9
• 题目数据保证列表表示的数字不含前导零

Related Topics

递归

链表

数学

👍 10822

👎 0

实现代码，链表算是我自己的一个短板。需要更加加强一下这块的练习。下面的结果是GPT给的答案。

package leetcode.editor.cn;
//java:两数相加
class P2AddTwoNumbers{
    public static void main(String[] args){
        Solution solution = new P2AddTwoNumbers().new Solution();
    }
    //leetcode submit region begin(Prohibit modification and deletion)
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode dummyHead = new ListNode(0); // 哑结点，便于返回结果
        ListNode current = dummyHead; // 当前节点指针
        int carry = 0; // 进位

        while (l1 != null || l2 != null) {
            int x = (l1 != null) ? l1.val : 0; // l1 的当前值
            int y = (l2 != null) ? l2.val : 0; // l2 的当前值
            int sum = carry + x + y; // 计算和
            carry = sum / 10; // 更新进位
            current.next = new ListNode(sum % 10); // 创建新节点
            current = current.next; // 移动当前指针

            if (l1 != null) l1 = l1.next; // 移动 l1 指针
            if (l2 != null) l2 = l2.next; // 移动 l2 指针
        }

        // 如果还有进位，添加新节点
        if (carry > 0) {
            current.next = new ListNode(carry);
        }

        return dummyHead.next; // 返回结果链表的头节点
    }
}
//leetcode submit region end(Prohibit modification and deletion)

}

最终的效果还是很好的

    class Solution {
        public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
            ListNode dummy = new ListNode(0);
            ListNode cur = dummy;
            int carry = 0;

            while (l1 != null || l2 != null){
                int x = l1 == null ? 0 : l1.val;
                int y = l2 == null ? 0 : l2.val;
                int sum = x + y + carry;
                carry = sum / 10;
                cur.next = new ListNode(sum % 10); //新节点是需要进位的
                cur = cur.next;
                if (l1 != null) l1 = l1.next;
                if (l2 != null) l2 = l2.next;
            }

            if (carry > 0){
                cur.next = new ListNode(carry);
            }
            return dummy.next;
        }
    }

由于对这个链表不熟悉，所以又手写了一遍，今天算法就到这里。明天再刷新一题。

2024-9-30 算法

给你一个字符串 s，找到 s 中最长的 回文 子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

提示：

• 1 <= s.length <= 1000
• s 仅由数字和英文字母组成

Related Topics

双指针

字符串

动态规划

👍 7365

👎 0

思路一：中心扩展法

• 从每个字符位置开始，尝试同时向左右扩展，寻找以当前字符或两个字符为中心的最长回文子串。
• expandAroundCenter 方法用于从中心开始扩展，判断左右字符是否相等。如果相等，继续扩展。
• 记录每次找到的最长回文子串的起始和结束位置，最终返回这个子串。

public class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) {
            return "";
        }
        
        int start = 0, end = 0;
        for (int i = 0; i < s.length(); i++) {
            int len1 = expandAroundCenter(s, i, i);   // 以单个字符为中心
            int len2 = expandAroundCenter(s, i, i + 1); // 以两个字符为中心
            int len = Math.max(len1, len2);
            if (len > end - start) {
                start = i - (len - 1) / 2;
                end = i + len / 2;
            }
        }
        return s.substring(start, end + 1);
    }

    private int expandAroundCenter(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            left--;
            right++;
        }
        return right - left - 1;
    }
}

内存情况

思路二： 动态规划

• 定义 dp[i][j]，表示字符串从 i 到 j 是否是回文。
• 初始化单个字符为回文，即 dp[i][i] = true。
• 通过比较 s[i] 和 s[j]，递归地判断内部子串是否是回文。
• 更新最长回文子串的长度和起始位置，最终返回最长的回文子串。

public class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 2) {
            return s;
        }

        int n = s.length();
        boolean[][] dp = new boolean[n][n];
        int maxLen = 1;
        int start = 0;

        // 单个字符的子串一定是回文
        for (int i = 0; i < n; i++) {
            dp[i][i] = true;
        }

        for (int len = 2; len <= n; len++) {  // len 为子串的长度
            for (int i = 0; i < n; i++) {
                int j = i + len - 1;
                if (j >= n) {
                    break;
                }

                if (s.charAt(i) == s.charAt(j)) {
                    if (len == 2) {
                        dp[i][j] = true;  // 两个字符相等的情况
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];  // 长度大于2时，依赖于子问题
                    }

                    if (dp[i][j] && len > maxLen) {
                        maxLen = len;
                        start = i;
                    }
                }
            }
        }

        return s.substring(start, start + maxLen);
    }
}

内存情况

总结

中心扩展法：时间复杂度为 O(n²)，空间复杂度为 O(1)。

动态规划法：时间复杂度为 O(n²)，空间复杂度为 O(n²)。